Nullstellen geben an, wo die Funktion die x-Achse schneidet. Hier ist also y=0.
Daher muss, um sie zu finden, die Funktion gleich null gesetzte werden.
\(f(x)=0=a\cdot x^2+b\cdot x+c\)
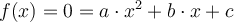
Wenn 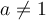\(a\neq 1\) ist, muss mit a dividiert werden und wir erhält:
\(0= x^2+\frac{b}{a}\cdot x+\frac{c}{a}\)
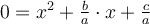
Häufig wird auch geschrieben:
\(0= x^2+p\cdot x+q\)
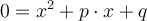
demnach gilt: 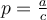\(p=\frac{a}{c}\) und \(q=\frac{b}{c}\)
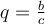
Die Nullstellen ergeben sich dann aus der pq-Gleichung:
\(x_0=-\frac{p}{2}\pm \sqrt{(\frac{p}{2})^2-q}\)
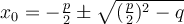
Es kann keine, eine oder zwei Nullstellen geben. Wenn es keine Nullstellen gibt, ist die Gleichung nicht lösbar.
