Abschnittsübersicht

◄08a-Strom
►10a-Energieübertragung

    • Lektion 1: Das Ölfilm-Experiment – Wie groß ist ein Molekül?

      In diesem Versuch möchten wir abschätzen, wie groß Moleküle sind – und zwar mithilfe eines Tropfens Öl auf Wasser. Aus einem winzig kleinen Tropfen entsteht ein hauchdünner Film, der uns verrät, wie dick (bzw. wie groß) ein einzelnes Molekül ist.

      1. Lernziel
      • Verstehen, wie man aus einem Ölfilm auf Wasser den Durchmesser eines Moleküls abschätzt.
      • Üben, mit einfachen Messwerten und Formeln zu rechnen.
      • Ein Gefühl dafür bekommen, wie winzig Atome und Moleküle sind.
      2. Hintergrundwissen
      • Moleküle sind winzige Teilchen, die sich aus mehreren Atomen zusammensetzen. Ihre Größe liegt im Bereich von 10⁻⁹ bis 10⁻¹⁰ Metern (Nanometerbereich).
      • Oktansäure ist eine Fettsäure, die im Wasser einen sehr dünnen Film bildet, weil ihre Moleküle nur eine Lage dick auf der Wasseroberfläche liegen.
      3. Materialien
      • eine flache Glasschale mit Wasser
      • Pipette oder Tropfflasche mit sehr verdünnter Oktansäure-Lösung in flüchtigem Öl
      • Lineal
      • Bärlappsamen
      4. Versuchsdurchführung

      1. Vorbereiten Fülle das Becherglas zu etwa drei Vierteln mit klarem Wasser und stelle es auf eine ebene Unterlage. Streue Bärlappsammen auf die Wasseroberfläche.

      2. Tropfen setzen Tauche die Pipette in die Öl-Lösung und setze einen einzigen Tropfen ganz vorsichtig auf die Wasseroberfläche. Achte darauf, dass keine zusätzlichen Tropfen ins Wasser gelangen!

      3. Film messen Warte kurz, bis sich das Öl gleichmäßig ausgebreitet hat und einen dünnen, kreisförmigen Film auf dem Wasser bildet. Miss nun den Radius r dieses Ölfilms.

      4. Tropfenvolumen schätzen Bei winzigeren Tropfen kannst du annehmen, dass ihr Volumen V etwa (0{,}05\;\text{cm}^3) beträgt.

      5. Berechnung des Moleküldurchmessers

      1. Fläche des Ölfilms Ein Kreis mit Radius r hat die Fläche

        A = \pi r^2.

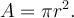
      2. Dicke des Films Weil der Tropfen sein Volumen V in eine schmale Scheibe umwandelt, gilt

        \text{Dicke } d = \frac{V}{A}.

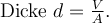
        Diese Dicke entspricht annähernd dem Durchmesser eines Moleküls.

      3. Rechenbeispiel

      • Gemessener Durchmesser des Ölfilms: \(r = 10{,}0\,\text{cm}\).

      • Tropfenvolumen: \(V = 0{,}05\,\text{cm}^3\).

        Fläche:

        A = \pi\,(10{,}0\,\text{cm})^2 = 100\pi\;\text{cm}^2 \approx 314{,}2\;\text{cm}^2.

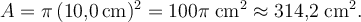
        Dicke:

        d = \frac{0{,}05}{314{,}2} \;\text{cm} \approx 1{,}59\times10^{-4}\;\text{cm} = 1{,}59\times10^{-6}\;\text{m}.

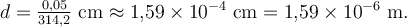
        Umgerechnet in Nanometer:

        1{,}59\times10^{-6}\,\text{m} = 1\,590\,\text{nm}.

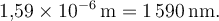
        Hinweis: Dieser Wert liegt etwas zu groß, weil unser Tropfenvolumen nur grob geschätzt ist. Typisch für Fettsäuremoleküle ist ein Durchmesser um \(2\,\text{nm}\). Trotzdem: Das Prinzip stimmt!

      6. Interpretation und Reflexion
      • Dein berechneter „Moleküldurchmesser“ zeigt, dass Moleküle millionenfach kleiner sind als Dinge die wir sonst messen.
      • Kleine Fehler in der Volumenschätzung oder der Messung des Durchmessers können das Ergebnis verändern. Eine Größenordnung kennen wir hierdurch aber.
      • Dieses Experiment verdeutlicht anschaulich, dass wir mit einfachen Mitteln auf sonst kaum zugängliche Größen schließen können.
    • 09.1a) Ölfilm-Versuch Test
      Teilnehmer/innen müssen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen

    • Lektion 2: Das Thomsonsche Atommodell – Der „Rosinenkuchen“ des Atoms

      1. Lernziel
      • Verstehen, wie J. J. Thomson Elektronen entdeckte und daraus sein Atommodell ableitete.
      • Erkennen der Stärken und Schwächen dieses frühen Atommodells.
      2. Hintergrundwissen
      • Elektronen sind negativ geladene Teilchen, die in Atomen vorkommen.
      • Positive Ladung muss im Atom vorhanden sein, um die negativen Elektronen zusammenzuhalten.
      3. Experimentelle Grundlage: Die Kathodenstrahlröhre
      1. Aufbau Eine evakuierte Glasröhre mit zwei Elektroden (Kathode und Anode). Schließt man eine hohe Spannung an, entstehen Strahlen von der Kathode zur Anode.
      2. Beobachtung
      • Diese Strahlen lassen einen Leuchtschirm auf der Röhrenwand aufleuchten.
      • Ablenkung durch elektrische und magnetische Felder zeigt: die Strahlen bestehen aus negativen Teilchen.
      1. Schlussfolgerung Thomson maß Ladung-zu-Masse-Verhältnis ($e/m$) dieser „Kathodenstrahlen“-Teilchen und fand: sie sind sehr viel leichter als alle bekannten Atome. Er nannte sie Elektronen.
      4. Thomson-Modell (1904)
      • Vorstellung: Atom besteht aus einer gleichmäßigen, positiven „Kuchenglobschaft“, in der viele kleine, negative Elektronen wie Rosinen eingebettet sind.
      5. Eigenschaften und Erklärungskraft
      • Elektrische Neutralität: Die Gesamtladung ist Null (positive Masse + negative Elektronen).
      • Einfaches Bild: Erklärt, warum Atome nach außen neutral erscheinen, aber trotzdem Ladungsträger (Elektronen) enthalten.
      6. Grenzen des Modells
      • Keine Erklärung für Streu-Experimente sehr energiereicher Teilchen.
      • Elektronenbewegung in einer statischen positiven Masse nicht genau beschrieben.
      • Spektrallinien von Atomen (z. B. im Wasserstoffspektrum) bleiben unerklärt.

    • Lektion 3: Rutherfords Atommodell – Der Atomkern wird ent­deckt

      1. Lernziel
      • Verstehen, wie Ernest Rutherford durch seine Goldfolie-Experimente den Atomkern nachwies.
      • Kennenlernen des experimentellen Aufbaus und der Auswertung der Messergebnisse.
      • Ableiten des neuen Atommodells mit Kern und Elektronenhülle.
      2. Hintergrundwissen
      • Streuung geladener Teilchen kann Aufschluss über die Verteilung der Ladung in einem Objekt geben.
      • α-Strahlung besteht aus positiv geladenen Helium-Kernen ($^{4}$He²⁺).
      3. Versuch: Streuung von α-Teilchen an Goldfolie
      1. Aufbau
      • Quelle für α-Teilchen auf einer Seite, extrem dünne Goldfolie in der Mitte.
      • Ringsförmige Leuchtschirm-Detektoren um die Folie herum.
      1. Beobachtung
      • Die meisten α-Teilchen fliegen gerade durch.
      • Einige werden stark abgelenkt, wenige bis zu fast 180° zurückgeworfen.
      1. Deutung
      • Die meiste Masse und positive Ladung eines Atoms muss in einem winzigen Volumen stecken (Kern).
      • Der Rest des Atoms ist großer, leerer Raum, in dem die Elektronen kreisen.
      4. Rutherford-Modell (1911)
      • Atomkern: Kleiner, dichter Kern mit fast der gesamten Masse und positiver Ladung.
      • Elektronenhülle: Viele Elektronen bewegen sich in der weiten, nahezu leeren Hülle um den Kern.
      5. Eigenschaften und Erklärungskraft

      • Erklärung der Streudaten:

        • Kaum Ablenkung → leere Hülle.
        • Große Ablenkung → dichter, geladener Kern.
      • Elektrische Neutralität weiterhin gegeben durch gleiche Gesamtzahl von Protonen im Kern und Elektronen außen.
      6. Grenzen des Modells
      • Bewegung der Elektronen nicht erklärt: klassische Bahnen würden Strahlung abgeben und kollabieren.
      • Spektrallinien (diskrete Emissionslinien) bleiben ohne Quantentheorie unerklärt.
    • 09.1b) Atommodelle Test
      Teilnehmer/innen müssen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen

    • Lektion 4: Aufbau des Atomskerns

      • Grundaufbau eines Atoms:

        • Protonen: Diese positiv geladenen Teilchen befinden sich im Atomkern und bestimmen, um welches Element es sich handelt. Zum Beispiel hat jedes Kohlenstoff-Atom 6 Protonen.
        • Neutronen: Diese Teilchen sind elektrisch neutral (haben keine Ladung) und befinden sich ebenfalls im Kern.
        • Elektronen: Diese negativ geladenen Teilchen kreisen um den Kern, aber sie spielen für die Isotopenbestimmung keine Rolle.

      • Ein Element

        • Bei einem bestimmten Element ist die Anzahl der Protonen immer gleich.
        • Die Anzahl der Neutronen kann jedoch variieren.

      • Ein Isotop

        • Ein Isotop ist eine Version eines Elements, bei der die Neutronenzahl festgelegt ist.
        • Von einem Element kann es also verschiedene Isotopen mit untereinander unter unterschiedlichen Neutronenzahlen geben.

        Beispiel:

        • Kohlenstoff-12: Besteht aus 6 Protonen und 6 Neutronen.
        • Kohlenstoff-14: Besteht aus 6 Protonen, aber 8 Neutronen.

      • Bedeutung

        • Chemische Eigenschaften: Da sich die chemischen Eigenschaften eines Elements durch die Protonen (und die Elektronen) bestimmen, verhalten sich Isotope chemisch quasi identisch.
        • Physikalische Eigenschaften: Die unterschiedlichen Neutronenzahlen verändern das Gewicht (die Masse) des Atoms. Einige Isotope sind instabil und zerfallen mit der Zeit, was in der Natur und in der Technik genutzt werden kann.

    • Lektion 5: Benennung und Aufschreiben von Isotopen

      Isotope können auf verschiedene Weise notiert werden.

      1. Nuklidschreibweise
        Hierbei werden die Massenzahl (A) (Anzahl der Protonen und Neutronen) und die Ordnungszahl (Z) (Anzahl der Protonen) in Form von hoch- und tiefgestellten Zahlen vor dem Elementsymbol geschrieben.
        Beispiel:

        • mit Massenzahl und Ordnungszahl: ^{14}_{6}\mathrm{C}
        • mit Massenzahl und ohne Ordnungszahl: ^{14}\mathrm{C}

      2. Element-Massenzahl-Darstellung (Bindestrich-Notation)
        Eine weitere übliche Darstellung ist die Verbindung des Elementsymbols mit der Massenzahl mittels eines Bindestrichs.
        Beispiele:

        • Mit abgekürzten Namen: C-14
        • Mit ausgeschriebenem Namen: Kohlenstoff-14
    • 09.1c) Schreibweise Isotopen-alle-Schreibweisen I Test
      Teilnehmer/innen müssen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
    • 09.1d) Schreibweise Isotopen-alle-Schreibweisen II Test
      Teilnehmer/innen müssen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
    • 09.1e) Schreibweise Isotopen Nuklidschreibweise I Test
      Teilnehmer/innen müssen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
    • 09.1f) Schreibweise Isotopen Nuklidschreibweise II Test
      Teilnehmer/innen müssen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen

    • Lektion 6: Die drei Arten radioaktiver Strahlung – α, β und γ

      1. Lernziel
      • Kennenlernen der drei grundlegenden Strahlungsarten: Alpha-, Beta- (β⁻ und β⁺) und Gammastrahlung.
      • Verstehen, wie jede Strahlung entsteht und welche Eigenschaften sie hat.
      • Einordnen der Durchdringungsfähigkeit und des Schutzbedarfs.


      2. Hintergrundwissen
      • Radioaktivität entsteht, wenn instabile Atomkerne zerfallen und dabei Energie in Form von Strahlung oder Teilchen freisetzen.
      • Die Zerfallsprodukte können geladene Teilchen (α, β⁻, β⁺) oder hochenergetische Photonen (γ) sein.


      3. Übersicht
      Strahlungsart Teilchen/Photon Ladung Masse (relativ) Geschwindigkeit Reichweite in Luft Abschirmung Beispielanwendung
      α Helium-4-Kern +2 ≈ 4 u ≈ 0,05 c wenige cm Papier, Haut Rauchmelder (²⁴¹Am)
      β⁻ Elektron −1 ≈ 5·10⁻⁴ u bis ≈ 0,9 c einige Meter 2–3 mm Aluminium/Plexiglas Dickenmessung in Folien/Papier
      β⁺ Positron +1 ≈ 5·10⁻⁴ u bis ≈ 0,9 c einige Meter 2–3 mm Aluminium + γ-Schutz Positronen-Emissions-Tomographie (PET)
      γ Photon 0 0 = c kilometerweit mehrere cm Blei oder dickes Beton Sterilisation, Krebstherapie
    • 09.1g) Aufbau Atomkern Test
      Teilnehmer/innen müssen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
      Bestehensgrenze erreichen oder alle verfügbaren Versuche ausschöpfen

    • Lektion 7: Die Nuklidkarte – Landkarte der Atomkerne

      1. Lernziel
      • Verstehen, was eine Nuklidkarte ist und wie man sie liest.
      • Erkennen, wie sich die Stabilität und Radioaktivität von Kernen in der Karte zeigen.
      • Lernen, wofür die Nuklidkarte in Forschung und Technik gebraucht wird.
      2. Hintergrundwissen
      • Nuklide sind genau definierte Atomkerne mit festgelegter Protonenzahl Z und Neutronenzahl N.
      • Jeder Kern hat eine bestimmte Masse, Ladung und unterschiedliche Stabilität.
      3. Aufbau der Nuklidkarte
      1. Achsensystem
      • Vertikale Achse (y-Achse): Protonenzahl Z (auch Ordnungszahl) – je weiter oben, desto mehr Protonen.
      • Horizontale Achse (x-Achse): Neutronenzahl N – je weiter rechts, desto mehr Neutronen.
      1. Kästchen für jeden Nukliden
      • Jedes Gitterfeld steht für ein Isotop also eine Kombination aus Neutronen und Protonen, also zum Beispiel 6 Protonen und 6 Neutronen für den Kohlenstoff-12-Kern.
      • Manchmal sind die Kästchen farbig markiert oder schraffiert, um Eigenschaften wie Stabilität, Halbwertszeit oder Art des radioaktiven Zerfalls zu zeigen.
      1. Stabile und instabile Kerne
      • Stabile Nuklide bilden eine Diagonale („Tal der Stabilität“) im mittleren Bereich der Karte ab.
      • Radioaktive Nuklide liegen ober- oder unterhalb dieser Linie. Ihre Kästchen werden oft anders eingefärbt (z. B. rot für α-Zerfall, grün für β-Zerfall).
      4. Nutzung und Information
      • Bestimmung von Zerfallsarten: Aus der Position oberhalb der Stabilitätslinie (zu viele Neutronen → β⁻-Zerfall) oder unterhalb (zu wenige Neutronen → β⁺-Zerfall oder Elektroneneinfang) kann man vorhersagen, wie ein instabiler Kern zerfällt.
      • Suche nach seltenen Kernen: Forscher markieren exotische Nuclide in entlegenen Bereichen der Karte, um sie in Teilchenbeschleunigern gezielt herzustellen.
      • Vergleich von Halbwertszeiten: Oft gibt ein Farbverlauf an, wie schnell ein Kern zerfällt – von Sekundenbruchteilen bis zu Milliarden Jahren.
      5. Beispiel: Kohlenstoff und Uran
      • Kohlenstoff-12 (Z=6, N=6) liegt genau auf der Stabilitätslinie und ist nicht radioaktiv.
      • C-14 (Z=6, N=8) hat zwei zusätzliche Neutronen, liegt oberhalb der Linie und zerfällt durch β⁻-Strahlung.
      • Uran-238 (Z=92, N=146) liegt weit rechts oben, zerfällt überwiegend α-Strahlung ab und hat eine Halbwertszeit von etwa \(4{,}5\times10^9\) Jahren.
      6. Interpretation der Karte
      • Ränder der Karte: Sehr neutronen- oder protonenreiche Kerne sind extrem kurzlebig und liegen am Rand; manche existieren nur für Bruchteile einer Sekunde.
      • Tal der Stabilität: Vom Koordinatenursprung nach rechts oben gehend liegt ein Bereich mit vielen stabilen Kernen.
      7. Anwendungen
      • Archäologie und Klimaforschung: C-14-Datierung nutzt die Position und Zerfallsdaten von Kohlenstoff-14.
      • Medizin: Radiopharmaka werden gezielt aus Nukliden ausgewählt, die passende Halbwertszeiten und Zerfallsarten besitzen.
      • Kerntechnik: Brennstoffzyklen und Abfallmanagement in Kernkraftwerken basieren auf Kenntnissen der Nuklidkarte.
    • 09.1h) Nuklidkarte Test
      Teilnehmer/innen müssen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen

    • Lektion 8: Halbwertszeit und Zerfallsgleichung

      • Verstehen, was die Halbwertszeit \(T_{1/2}\) eines radioaktiven Stoffes bedeutet.
      • Die Zerfallsgleichung anwenden können.
      • Üben, mit der Basis \(\tfrac12\) und Exponentialfunktionen zu rechnen.
      2. Hintergrundwissen
      • Radioaktiver Zerfall ist ein zufälliger Prozess: Jedes instabile Nuklid hat eine bestimmte Wahrscheinlichkeit, in einem Zeitintervall zu zerfallen.
      • Halbwertszeit \(T_{1/2}\): Zeitspanne, in der genau die Hälfte aller vorhandenen Kerne zerfallen ist.
      3. Definition: Halbwertszeit

      • Nach einer Zeit \(t = T_{1/2}\) bleibt von der Anfangsmenge \(N_0\) nur noch

        N = \frac{N_0}{2} = N_0\cdot\Bigl(\tfrac12\Bigr).

      • Nach zwei Halbwertszeiten \(2\cdot T_{1/2}\) ist nur noch ein Viertel übrig:

        N = N_0\cdot\Bigl(\tfrac12\Bigr)^2 = N_0\cdot\frac14.

      4. Zerfallsgleichung

      Die Zerfallsgleichung lautet:

      N(t)=N_0 \cdot (\frac{1}{2})^{\frac{t}{T_{1/2}}}

      Hierbei ist:

      • \(N(t)\) die Stoffmenge zum Zeitpunkt t
      • \(N_0\) die Stoffmenge zum Zeitpunkt \(t=0s\)
      • \(t\) die Zeit
      • \(T_{1/2}\) die Halbwertszeit.

      5. Beispielrechnung
      • Gegeben: Anfangsmenge \(N_0 = 800\) Kerne, Halbwertszeit \(T_{1/2} = 5\) Jahre.
      • Aufgabe: Wie viele Kerne sind nach \(t = 12\) Jahren noch vorhanden?

      1. Setze in die Gleichung ein:

        N(12) = 800 \;\Bigl(\tfrac12\Bigr)^{\frac{12}{5}} = 800 \;\Bigl(\tfrac12\Bigr)^{2{,}4}.

      2. Berechne den Exponenten: \(\bigl(\tfrac12\bigr)^{2{,}4} \approx 2^{-2{,}4} \approx 0{,}189\).

      3. Ergebnis:

        N(12) \approx 800 \times 0{,}189 \approx 151 \;\text{Kerne}.

      6. Interpretation
      • Schon nach etwas mehr als zwei Halbwertszeiten (hier: \(2 \times 5 = 10\) Jahre) ist die Menge auf unter ein Viertel geschrumpft.
      • Der Zerfall verlangsamt sich nicht linear, sondern exponentiell: Je mehr Kerne zerfallen sind, desto langsamer nimmt die restliche Menge ab.
      7. Anwendung
      • C-14-Datierung: Halbwertszeit von \(\approx 5730\) Jahren.
      • Medizinische Radioisotope: Auswahl nach passender Halbwertszeit, z. B. Tc-99m mit \(T_{1/2}\approx6\) Stunden für Diagnostik.
      • Strahlenschutz: Abschätzung, wie lange Radioaktivität ein Risiko darstellt.
    • 09.1i) Aufstellen der Zerfallsgleichung Test
      Teilnehmer/innen müssen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
    • 09.1j) Umstellen und lösen der Zerfallsgleichung Test
      Teilnehmer/innen müssen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
◄08a-Strom
►10a-Energieübertragung