Abschnitt: 4) Wurzelfunktionen | Mathe Sek2-11 4) Funktionen

Abschnittsübersicht

- Aktivität Wurzelfunktionen auswählen
  
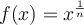
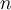
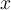
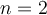
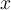
  Wurzelfunktionen sind spezielle Potenzfunktionen der Form $f(x) = \sqrt[n]{x}$ oder äquivalent $f(x) = x^{\frac{1}{n}}$ , wobei $n$ eine positive ganze Zahl ist. Diese Funktionen ordnen jeder positiven Zahl $x$ ihre n-te Wurzel zu. Für $n = 2$ handelt es sich um die Quadratwurzelfunktion, die jeder positiven Zahl $x$ ihre positive Quadratwurzel zuordnet. 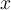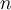Wurzelfunktionen sind im Allgemeinen nur für nicht-negative $x$ definiert (wenn $n$ gerade ist) und ihr Graph verläuft im ersten Quadranten des Koordinatensystems. 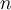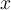Bei ungeraden $n$ sind Wurzelfunktionen für alle reellen $x$ definiert.