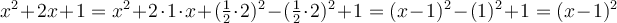Abschnittsübersicht

◄3) Allgemeine Form
►5) Stauchung und Streckung

    • Um aus der Scheitelpunktform in die allgemeine Form zu kommen, muss die Klammer ausmultipliziert werden.

      Um von der allgemeinen Form zur Scheitelpunktform zu kommen, ist die Umformung komplizierter.
      Der Term muss so vorbereitet werden, dass ein Teil von ihm die Struktur der rechten Seite der binomischen Formel hat:

      \(x^2+bx+c=x^2+2\cdot \frac{1}{2} b\cdot x+(\frac{1}{2}b)^2-(\frac{1}{2}b)^2+c=(x-\frac{1}{2}b)^2-(\frac{1}{2}b)^2+c\)

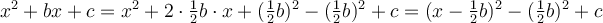
      Beispiel:

      \(x^2+2x+1=x^2+2\cdot 1\cdot x+(\frac{1}{2}\cdot 2)^2-(\frac{1}{2}\cdot 2)^2+1=(x-1)^2-(1)^2+1=(x-1)^2\)

    • 4a) quadratische Ergänzung Hinleitungteil 1 Test
      Teilnehmer/innen müssen
      Anzeigen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
    • 4b) quadratische Ergänzung Hinleitungteil 2 Test
      Teilnehmer/innen müssen
      Anzeigen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
    • 4c) quadratische Ergänzung Hinleitungteil 3 Test
      Teilnehmer/innen müssen
      Anzeigen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
    • 4d) quadratische Ergänzung Hinleitungteil 4 Test
      Teilnehmer/innen müssen
      Anzeigen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
    • 4e) quadratische Ergänzung Hinleitungteil 5 Test
      Teilnehmer/innen müssen
      Anzeigen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
    • 4f) quadratische Ergänzung Hinleitungteil 6 Test
      Teilnehmer/innen müssen
      Anzeigen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
    • 4g) quadratische Ergänzung I Test
      Teilnehmer/innen müssen
      Anzeigen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
    • 4g) quadratische Ergänzung II Test
      Teilnehmer/innen müssen
      Anzeigen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
◄3) Allgemeine Form
►5) Stauchung und Streckung