1) Sinus, Kosinus und Tangens im rechtwinkligen Dreieck

Gesetze im Dreieck:

Winkelsumme: In einem Dreieck beträgt die Summe der Innenwinkel stets 180 Grad. Mathematisch ausgedrückt: \(\alpha + \beta + \gamma = 180^\circ\), wobei \(\alpha\), \(\beta\) und \(\gamma\) die Innenwinkel des Dreiecks sind.

Sinussatz: Der Sinussatz besagt, dass das Verhältnis zwischen der Länge einer Seite \(a\), die dem Winkel \(\alpha\) gegenüberliegt, und \(\sin(\alpha)\) gleich der Länge einer anderen Seite \(b\) und \(\sin(\beta)\) ist:
\(\frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)}\)
\(\iff\frac{a}{b} = \frac{\sin(\alpha)}{\sin(\beta)}\)

Kosinussatz: Der Kosinussatz besagt, dass in einem Dreieck mit den Seitenlängen \(a\), \(b\) und \(c\) und den jeweils gegenüberliegenden Winkeln \(\alpha\), \(\beta\) und \(\gamma\) gilt:
\(a^2 = b^2 + c^2 - 2bc\cos(\alpha)\)
\(b^2 = b^2 + c^2 - 2bc\cos(\beta)\)
\(c^2 = a^2 + b^2 - 2ab\cos(\gamma)\)

Gesetze im rechtwinkligen Dreieck:

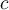
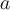
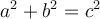
Satz des Pythagoras: Der Satz des Pythagoras besagt, dass in einem rechtwinkligen Dreieck das Quadrat der Länge der Hypotenuse (\(c\)), gleich der Summe der Quadrate der Längen der beiden anderen Seiten (\(a\) und \(b\)) ist. Dies kann als \(a^2 + b^2 = c^2\) ausgedrückt werden.

Sinus, Kosinus und Tangens: Diese Funktionen helfen, die Verhältnisse zwischen den Seitenlängen und Winkeln eines rechtwinkligen Dreiecks zu berechnen.
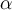
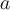
Der Sinus eines Winkels (\(\alpha\)) ist das Verhältnis der Länge der Seite gegenüber dem Winkel (\(a\)) zur Länge der Hypotenuse (\(c\)):
\(\sin \alpha = \frac{a}{c}\).
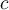
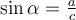
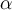
Der Kosinus eines Winkels (\(\alpha\)) ist das Verhältnis der Länge der Kathete neben dem Winkel (\(b\)) zur Länge der Hypotenuse (\(c\)):
\(\cos \alpha = \frac{b}{c}\).
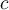
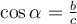
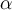
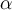
Der Tangens eines Winkels (\(\alpha\)) ist das Verhältnis der Länge der Seite gegenüber dem Winkel (\(\alpha\)) zur Länge der Kathete neben dem Winkel (\(b\)):
\(\tan \alpha = \frac{a}{b}\).

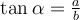
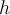
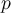
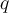
Höhensatz: Der Höhensatz besagt, dass die Länge der Höhe (\(h\)), die von der rechten Winkel des Dreiecks zu der Hypotenuse gezogen wird, das Produkt der Längen der beiden Abschnitte der Hypotenuse (\(p\) und \(q\)) ist, die von den Füßen der Höhe begrenzt werden: \(h^2 = p \cdot q\).

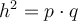
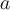
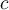
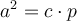
Kathetensatz: Der Kathetensatz besagt, dass das Quadrat der Länge einer Kathete (\(a\) oder \(b\)) gleich dem Produkt aus der Länge der Hypotenuse (\(c\)) und dem Abschnitt der Hypotenuse ist, der vom Fuß der Höhe bis zur Kathete reicht: \(a^2 = c \cdot p\) oder \(b^2 = c \cdot q\).

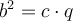
Diese Gesetze können bei der Berechnung von Seitenlängen oder Winkeln eines rechtwinkligen Dreiecks nützlich sein.