Abschnittsübersicht

◄1) Ableitungen - Ketten- und Produktregel
►3) natürlicher Logarithmus

    • Exponentielle Funktionen ergeben abgeleitet wieder exponentielle Funktionen.

      Dies ist eine Besonderheit im Gegensatz zu den meisten anderen Funktionen.

      \(f(x)=b^x\)

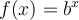
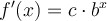      \(f'(x)=c\cdot b^x\) mit einer Konstanten c.

      Durch geschickte Wahl von b ist es möglich c=1 zu erhalten.

      Dann gilt f(x)=f'(x).

      Hierzu muss b die sogenannte eulersche Zahl e sein.

      e ist wie π eine transzendente Zahl, sie kann z.B. nicht vollständig als Bruch oder als Kommazahl dargestellt werden.

      e≈2,71828182846≈2,72


    • 2a) Eine besondere exponential Gleichung Test
      Teilnehmer/innen müssen
      Anzeigen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
    • 02b) Wechsel der Darstellungsform bei e-Funktionen Test
      Teilnehmer/innen müssen
      Anzeigen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
    • 02c) Ableitung der e-Funktion (Kettenregel) Test
      Teilnehmer/innen müssen
      Anzeigen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
    • 02d) Ableitung der e-Funktion (Produktregel) Test
      Teilnehmer/innen müssen
      Anzeigen
      Eine Bewertung erhalten
      Bestehensgrenze erreichen
◄1) Ableitungen - Ketten- und Produktregel
►3) natürlicher Logarithmus