Mithilfe des Konferenzintervalls kann der Bereich, innerhalb dessen der wahre Parameter einer Grundgesamtheit liegt, aus einer Stichprobe heraus abschätzt werden.
Hierbei liegt der Parameter mit einer vorgegebenen Wahrscheinlichkeit innerhalb des Bereiches.
Unter der Annahme einer binominal verteilten Größe, die sich durch eine Normalverteilung annähern lässt, gilt:
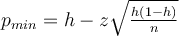
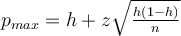
hierbei ist p die Trefferwahrscheinlichkeit in der Gesamtpopulation, h die relative Trefferhäufigkeit in der Stichprobe, n die Größe der Stichprobe und z der die Sicherheitswahrscheinlichkeit bestimmende Faktor.