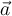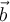Vektoren \(\vec{a}\) und \(\vec{b}\) sind genau dann linear abhängig voneinander, wenn es einen Faktor 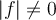\(|f|\neq 0\) gibt mit dem gilt:
\(f\cdot\vec{a}=f\cdot\left(\begin{array}{c} x_1 \\ y_1 \\ z_1
\end{array}\right)=\left(\begin{array}{c} f\cdot x_1 \\ f\cdot y_1 \\ f\cdot z_1
\end{array}\right)=\left(\begin{array}{c} x_2 \\ y_2 \\ z_2 \end{array}\right)=\vec{b}\)
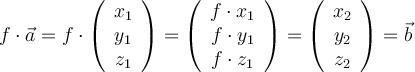
Beide Vektoren zeigen genau dann in die gleiche Richtung, wenn f positiv ist. Sie zeigen genau dann in
entgegengesetzte Richtungen, wenn f negativ ist.
Wenn 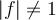\(|f|\neq 1\) ist, haben die Vektoren unterschiedliche Längen. Wenn zusätzlich 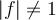\(|f|\neq 1\) ist, sind sie linear abhängig voneinander. Die Vektoren haben dann unterschiedliche Längen.
Die Vektoren heißen linear unabhängig, wenn es kein solches f gibt.
